Kalkulator odchylenia standardowego

Enter Inputs	5,20,40,80,100 Enter the Numbers with Comma separated(,)

Result:
No.of Inputs
Mean
Standard Deviation(SD)
Population Standard Deviation(PSD)
Variance(SD)
Variance(PSD)
Calculation

Kalkulator odchylenia standardowego do obliczania wspólnej miary rozprzestrzeniania się zestawu danych, jest analiza danych. Kalkulator może dać nr nakrycia, średnie, odchylenie standardowe (SD), odchylenie standardowe Ludności (PSD), wariancję (SD), wariancję (PSD) danych wartości wejściowych zestawu danych.

Formuła odchylenia standardowego

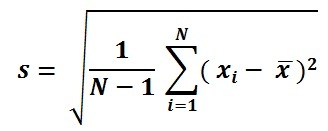
Standard Deviation Formula & Calculation

Formuła SD ludności

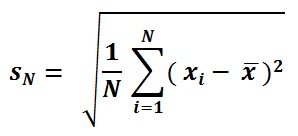
PSD - Population Standard Deviation Formula & Calculation

Formuła wariancji.

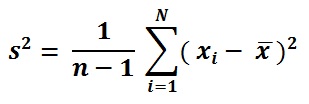
Variance Formula & Calculation

Średnia formuła

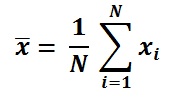
Mean Formula & Calculation

Na przykład, podając zestaw danych 5,20,40,80,100 , wynik będzie:

.

Całkowite wejścia (N) = (5,20,40,80,100)

Całkowite wejścia (N) = 5

Średnia (xm) = (x1 + x2 + x3 ... xn) / n

Średnia (xm) = 245/5

Środki (XM) = 49

-------------------------------------------

Sd =.

SQRT (1 / (N-1) * (X1-XM) ^ 2 + (X2-XM) ^ 2 + .. + (XN-XM) ^ 2))

= SQRT (1 / (5-1) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2 ))

= SQRT (1/4 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRT (1/4 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1605)

= 40.0625.

Wariancja = sd ^ 2

Wariancja = 40.0625 ^ 2

Wariancja = 1605.

-------------------------------------------

PSD =.

SQRT (1 / (N) * ((X1-XM) ^ 2 + (X2-XM) ^ 2 + .. + (XN-XM) ^ 2))

= SQRRT (1 / (5) ((5-49) ^ 2 + (20-49) ^ 2 + (40-49) ^ 2 + (80-49) ^ 2 + (100-49) ^ 2))

= SQRT (1/5 ((- 44) ^ 2 + (- 29) ^ 2 + (- 9) ^ 2 + (31) ^ 2 + (51) ^ 2))

= SQRRT (1/5 ((1936) + (841) + (81) + (961) + (2601)))

= SQRT (1284)

= 35.8329.

Wariancja = sd ^ 2

Wariancja = 35.8329 ^ 2

Wariancja = 1284.

Kalkulator odchylenia standardowego

FoxCalculators - Darmowe kalkulatory online!