Eigenvektory i obliczanie EIGENVALUES

Regular Matrix A =
Identity Matrix I =
Scalar Matrix(Z=c×I)
c =
|A| =
Singular Matrix (A - c×I) =
|A - c×I| =
Trace of A =
Eigen Value (c2) =
Eigen Value (c1) =
c1 in Eigen Vector x1 value =
c2 in Eigen Vector x1 value =
c1 in Eigen Vector x2 value =
c2 in Eigen Vector x2 value =

Ejhenvector kwadratowej matrycy A jest niezerowy wektor V, gdy V = λ V, λ nazywany jest wartością wartości własnej odpowiadającej v.

Wszystkie własne wartości własne i EIGENVECTORS spełniają równanie AX = λx dla danej matrycy kwadratowej A.

Online Eigenvectors i Kalkulator EIGENVALUES mogą uzyskać | A |, pojedyncza matryca (A - C × I), ślad A, wartość Eigen Matrix A

Na przykład

Dla matrycy.

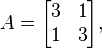
wektor

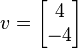
jest EIGENVECTOR z EIGENVALUE 2.

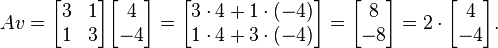
Z drugiej strony wektor

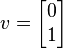
jest nie EIGENVECOR, ponieważ

.

.

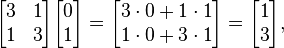
A ten wektor nie jest wielokrotnością oryginalnego wektora v.

Eigenvektory i obliczanie EIGENVALUES
Kalkulatory rekomendacji Torque do konwertera konwertera Kalkulator jednostek zużycia paliwa Solver Capture Prędkość powietrza Kalkulator przepływu kanału powietrza Kalkulator konwertera przepływu. Kalkulator utraty rur wodnych Kalkulator prędkości przewodu powietrznego Siła hydrauliczna i wału kalkulatora pompy Kalkulator wiązki obsługuje Sprężone linie rurowe Speed ​​to Converter Kalkulator panelu słonecznego. Kalkulator odchylania belek stałych Prawo Ohm z kalkulatora mocy Kalkulator utraty głowicy przepływu powietrza