Kalkulator stałej powierzchni |
| a = | |
| r = | |
| Units: | |
| Surface Area = | 0 |
 a = side length
a = side lengthr = radius
Okrągła powierzchnia stożka
- .
Boczna powierzchnia = Πrrs = πr√ (r 2 + h 2 )
Powierzchnia podstawy = πr 2
Całkowita powierzchnia
= L + B = Πrrs + πr 2 = πr (s + r) = πr (R + √ (R 2 + h 2 ) )
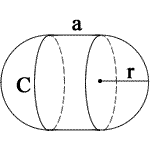
Powierzchnia kapsułki
- .
Powierzchnia = 2rrr (2r + a)
Okrągła powierzchnia cylindra
- .
Górna powierzchnia = πr 2
Dolna powierzchnia = πr 2
Całkowita powierzchnia
= L + T + B = 2πRH + 2 (πr 2 ) = 2πR (H + R)
Obszar powierzchni kostki
- .
Powierzchnia = 6a 2
Stożkowa powierzchnia frustum
- .
Powierzchnia boczna
= π (R 1 + R 2 ) S = π (R 1 + R 2 ) √ (( R 1 - R 2 ) 2 + h 2 )
Powierzchnia górna = πr 1 2
Powierzchnia podstawy = πr 2 2
Całkowita powierzchnia
= π (R 1 2 + r 2 2 + (r 1 * * r 2 ) * s)
= π [R 1 2 + r 2 2 + (r 1 * * r 2 ) * √ ((R 1 - R 2 ) 2 + h 2 )]
Powierzchnia półkuli
- .
Zakrzywiona powierzchnia = 2πr 2
Powierzchnia podstawy = πr 2
Całkowita powierzchnia = (2πR 2 ) + (πr 2 ) = 3πr 2
Prostokątna powierzchnia pryzmatu
- .
Powierzchnia = 2 (LW + LH + WH)
Powierzchnia piramidowa
- .
Powierzchnia boczna = A√ (A 2 + 4H 2 )
Powierzchnia podstawy = 2
Całkowita powierzchnia
= L + B = a 2 + a√ (A 2 + 4H 2 ))
= a (A + √ (a 2 + 4H 2 ))
Sferyczna powierzchnia czapek
- .
Powierzchnia = 2πrh
Kula powierzchnia
- powierzchnia = 4πr 2
Na przykład, aby sfera, gdy r = 3
- .
Aby obliczyć powierzchnię sfery, użyj następującego wzoru: 4πR 2 . Gdy substytutujesz R dla jego wartości, otrzymasz 4π * 3 2 , co równa się 113.09734 m 2 .
Na przykład, do stożka, gdy r = 3, h = 3
- .
Aby obliczyć powierzchnię stożka, użyj następującego wzoru: πR (R + √ (R 2 + h 2 )). Gdy zastępujesz R i H za ich wartości, otrzymujesz π3 (3 + * radic; (3 2 + 3 2 )), który wynosi 68,26028 m 2 .
wybór języka:日本語 | 한국어 | Français | Español | ไทย| عربي | русский язык | Português | Deutsch| Italiano | Ελληνικά | Nederlands | Polskie| Tiếng Việt| বাংলা| Indonesia| Pilipino| Türk| فارسی| ລາວ| ဗမာ| български| Català| čeština| Қазақ| Magyar| Română| Україна
Copyright ©2021 - 2031 All Rights Reserved.