Kartezjański równanie kalkulatora samolotu

Point A , ,
Point B , ,
Point C , ,
   
Equation of the plane
(given three points)		 x+y+z+=0

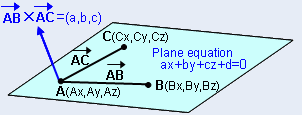
Istnieją trzy punkty A (X 1 , Y 1 , z 1 ), b (x 2 y 2 , z 2 ) i C (x 3 , Y 3 , z 3 ) Leżący na płaszczyźnie, a następnie równanie płaszczyzny można znaleźć za pomocą następującej wzoru

.

.

.

.

x - x 1

y - y 1

z - z 1

= 0

x 2 - x 1

y 2 - y 1

z 2 - Z 1

x 3 - x 1

y 3 - y 1

z 3 - z 1

Lub (AS, AY, AZ), B (BX, BZ), C (CX, C CZ), równanie płaszczyzny jest AX + przez + CZ + D = 0

Gdzie,

a = (by-ay) (CZ-AZ) - (CY-AY) (BZ-AZ)

B = (BZ-AZ) (CX-AX) - (CZ-AZ) (BX-AX)

C = (BX-AY) (CY-AY) - (CX-AY) (By-Ay)

D = - (AAX + Bay + CAZ).

Obliczanie równania samolotu kartezjańskiego z trzema współrzędnymi jest tutaj łatwiejszy.

Kartezjański równanie kalkulatora samolotu
Kalkulatory rekomendacji Torque do konwertera konwertera Kalkulator jednostek zużycia paliwa Solver Capture Prędkość powietrza Kalkulator przepływu kanału powietrza Kalkulator konwertera przepływu. Kalkulator utraty rur wodnych Kalkulator prędkości przewodu powietrznego Siła hydrauliczna i wału kalkulatora pompy Kalkulator wiązki obsługuje Sprężone linie rurowe Speed ​​to Converter Kalkulator panelu słonecznego. Kalkulator odchylania belek stałych Prawo Ohm z kalkulatora mocy Kalkulator utraty głowicy przepływu powietrza